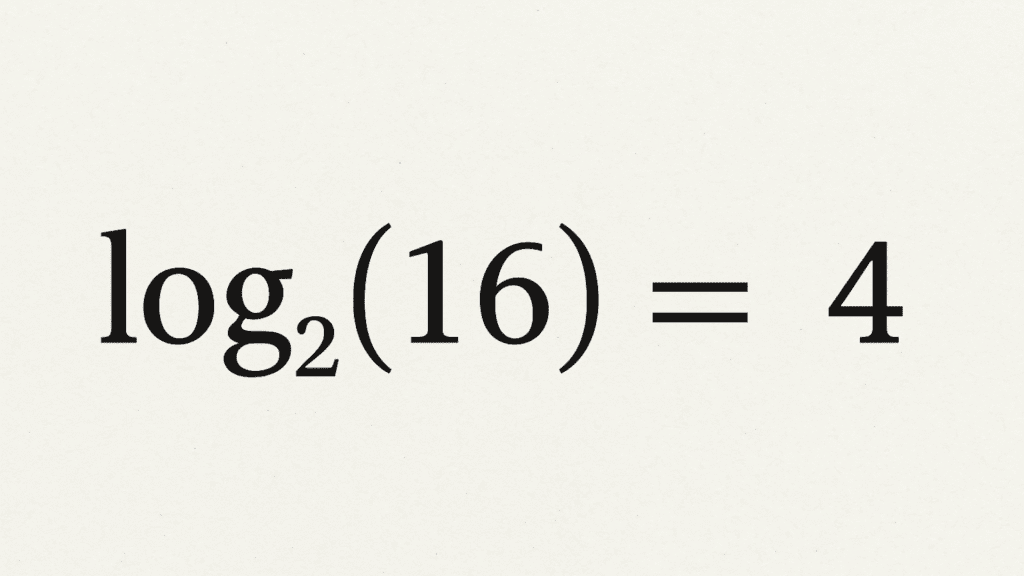O cálculo de logaritmos, ou simplesmente “log”, pode parecer um mistério para muitos, mas é uma ferramenta essencial na matemática e em diversas áreas do conhecimento. Seja em cálculos científicos, estudos de crescimento exponencial ou algoritmos de segurança digital, os logs são fundamentais para simplificar operações e interpretar dados. Quer entender como calcular log de forma clara e prática? Acompanhe este guia e descubra como essa função pode facilitar sua vida acadêmica e profissional.
O que é logaritmo e por que ele é tão importante?
Em termos simples, o logaritmo de um número é o expoente ao qual uma base fixa deve ser elevada para obter esse número. Por exemplo, o logaritmo de 1000 na base 10 é 3, pois 10³ = 1000. Ele inverte o processo da exponenciação e ajuda a resolver equações complexas de forma mais intuitiva.
A importância do logaritmo vai além da matemática pura. Ele aparece em ciências exatas, em análises financeiras, na computação e até em estatísticas avançadas. Desde medir a intensidade de terremotos até calcular taxas de crescimento em economia, o log é um aliado poderoso para compreender grandezas em escala.
Como calcular log na prática
Existem dois tipos principais de logaritmos: o logaritmo decimal (ou logaritmo comum, de base 10) e o logaritmo natural (de base “e”, conhecido como “ln”). A fórmula geral para calcular log é:
log_b (x) = y
Onde:
- b = base do logaritmo
- x = número desejado
- y = resultado (expoente)
Exemplo prático para logaritmo na base 10:
log₁₀ (100) = 2, porque 10² = 100.
No caso do logaritmo natural, usamos a base “e” (aproximadamente 2,718). Por exemplo:
ln (e²) = 2.
Ferramentas e estratégias para calcular log
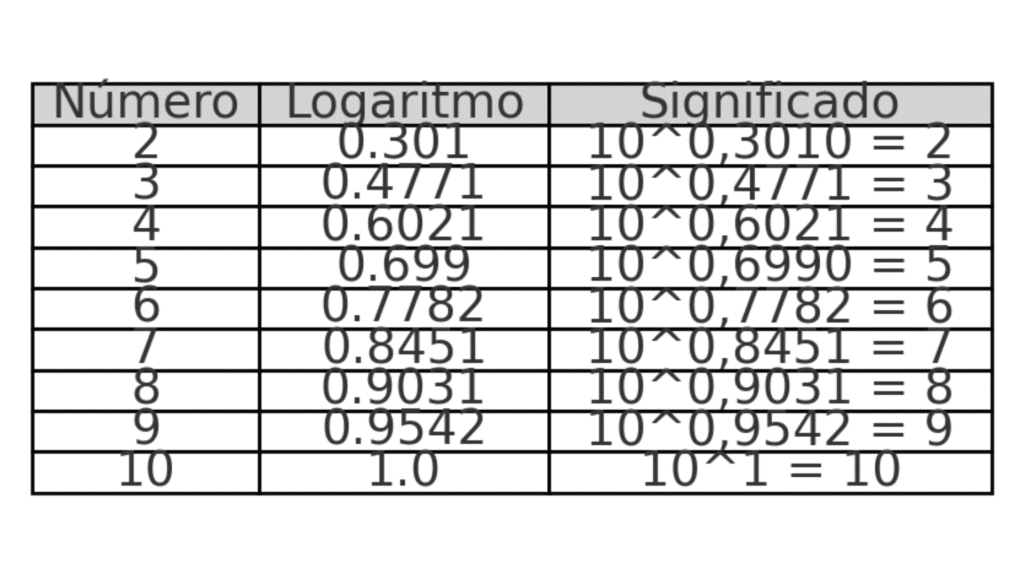
Para cálculos manuais, é possível usar tabelas logarítmicas, mas atualmente, as calculadoras científicas e aplicativos digitais fazem esse trabalho de forma instantânea. Basta digitar o número desejado e pressionar a tecla “log” ou “ln”, dependendo da base que deseja usar.
Outra alternativa muito útil é o uso de planilhas eletrônicas, como o Excel. As funções “=LOG10(x)” ou “=LN(x)” permitem cálculos rápidos e automáticos, facilitando análises de dados e simulações complexas.
Principais aplicações dos logaritmos
Além de facilitar cálculos matemáticos, o logaritmo aparece em situações do cotidiano e em áreas de pesquisa. Ele está presente em:
- Escalas de intensidade sonora (decibéis)
- Crescimento populacional e demografia
- Análises financeiras e juros compostos
- Algoritmos criptográficos e de compressão de dados
- Medidas de pH em química
Essas aplicações mostram como o log não é apenas uma ferramenta abstrata, mas um conceito prático e essencial em várias áreas do conhecimento.
Compreender como calcular log não é apenas um passo importante para quem estuda matemática ou física, mas uma habilidade prática que amplia o entendimento de fenômenos que moldam nosso mundo. Use calculadoras, planilhas ou aplicativos digitais como aliados para dominar essa ferramenta e aproveite todo o potencial dos logaritmos em sua rotina de estudos ou trabalho. Afinal, o log é mais do que um número: é um caminho para o conhecimento.
Leia também:
- 5 igrejas em lugares inusitados que encantam e surpreendem
- Como a literatura de cordel mantém viva a cultura popular brasileira
- Como a física quântica influencia a minha vida cotidiana
- Como fazer Bottons um guia criativo